Sujet du DS et correction

Dans la première partie du sujet on redémontre l'algorithme de Newtow. On calcule aussi la vitesse de convergence. 

Dans la deuxième partie, on montre que la suite donnée par $\cos(n)$ ne converge pas mais qu'elle converge au sens de Cesàro.

(Cliquez sur les images pour avoir une meilleure définition)

---

---

---

---

---

---

Une taupe sur mars le 26 novembre ! - English

Sur l'accordage des instruments

Vidéo très bien faite sur les problèmes (et la solution moderne !) d'accordage des instruments.

Approximation de ln(2) - méthode des trapèzes

Nous continuons le brassage des techniques de calculs (qui ne sera pas exhaustive...) de $\ln(2)$. On a vu dans le post précédent que l'on peut voir
\[\ln(2)=\int_0^1 \frac{1}{1+x}dx.\]

Il y existe toute une "jungle" de méthode d'approximation pour le calcul d'une intégrale. Stricto-senso, les sommes de Riemann sont au programme de l'écris du CAPES et pas les autres méthodes.

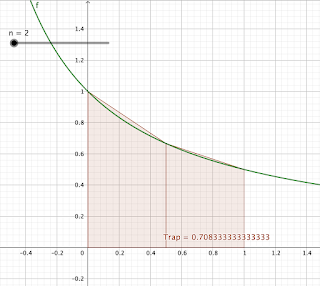
Parlons rapidement de la méthode des trapèzes. Comme on peut le deviner, au lieu d'approcher l'aire à l'aide de rectangles, on s'aide de trapèzes. On peut consulter wiki pour une introduction.

Ces deux méthodes sont implémentées dans geogebra : SommeRectangles et SommeTrapèzes.

Etant donnée une fonction $f$ continue sur $[a,b]$, pour $\int_a^b f(x)\,dx$, avec $n\in \mathbb{N}$, on l'approche par 

\[S_n(f):=\frac{b-a}{n} \left( {f(a) + f(b) \over 2} + \sum_{k=1}^{n-1} f \left( a+k \frac{b-a}{n} \right) \right)\]

Si $f\in C^2([a,b])$, grâce au théorème des accroissements finis, il n'est pas très difficile de montrer que

\[\left|\int_a^b f(x)\,dx - S_n(f)  \right| \leq \frac{(b-a)^3}{12n^2}\max_{x\in [a,b]}|f''(x)|.\]

Contrairement à la méthode des rectangles, celle-ci est d'ordre $2$. Cependant elle s'appuie sur une hypothèse un peu plus forte, $C^2$ au lieu de $C^1$.

Revenons à notre exemple fil rouge. On a

\[S_n^{trap}:=\frac{1}{n} \left( \frac{3}{4} + \sum_{k=1}^{n-1} \frac{1}{1+ \left( \frac{k}{n} \right) }\right) = \frac{3}{4n} + \sum_{k=1}^{n-1} \frac{1}{n+ k}\]

avec une erreur de

\[\frac{1}{6n^2}.\]

Pour avoir une précision à $10^{-9}$ près il suffit de prendre $n\geq \sqrt{10^9/6}\geq 12910$. Cela est vraiment meilleur que pour la méthode des rectangles qui demandait $10^9$ termes pour la même précision. Cependant, cela reste encore très grand comme nombre.

On rappelle qu'avec la méthode des rectangles on avait obtenu:

\[S_n^{rect}:=\sum_{k=1}^{n} \frac{1}{n+ k}.\]

Si l'on compare les deux on obtient:

\[S_n^{trap} = S_n^{rect} -\frac{1}{4n}.\] 

On peut résumer cette comparaison par :

\begin{align*}\ln(2)&= \sum_{k=1}^{n} \frac{1}{n+ k} + O\left(\frac{1}{n}\right)\\ &=-\frac{1}{4n} + \sum_{k=1}^{n} \frac{1}{n+ k} + O\left(\frac{1}{n^2}\right), \end{align*}

quand $n\to \infty$. Cela rappelle fortement un développement limité...

Pour aller plus loin on pourra par exemple consulter le site de Serge Mehl et regarder la méthode de Simpson qui est d'ordre 4. 

Approximation de ln(2) par les sommes de Riemann

Nous allons maintenant changer de stratégie et approcher $\ln(2)$ à l'aide d'une autre suite. 

On commence par un rappel. Soit $f\in C([a,b])$ et $n\in \mathbb{N}^*$, on pose 

\[S_n(f):= \frac{1}{n}\sum_{k=1}^n f(a + k(b-a)/n).\]

Quand $n\to\infty$, on a que $S_n$ tend vers $\int_a^b f(t) dt$. Voir par exemple ici pour une preuve. En fait $S_n$ est une somme de Riemann associé à $f$, elle correspond à prendre la valeur de $f$ aux points de droite (car la somme commence par 1 et fini par $n)$ pour approcher l'intégrale. Pour avoir les points de gauche, il aurait fallut prendre $k=0,...,(n-1)$.

Considérons $f(x):=\frac{1}{1+x}$ sur $[0,1]$. On voit que $\int_0^1 f(t) dt= \ln(2)$ qui est la valeur qui nous intéresse. La suite $S_n$ est donnée, quant à elle, par 

\[S_n= \frac{1}{n} \sum_{k=1}^n \frac{1}{1+ k/n}=  \sum_{k=1}^n \frac{1}{n+ k}.\]

Il nous reste à estimer l'erreur d'approximation. On pose $x_k:= 1+k/n$. On utilise le théorème des accroissements finis sur chaque intervalle $[x_k, x_{k+1}]$. On obtient :

\begin{align*}|S_n - \ln(2)|&= \left|\frac{1}{n} \sum_{k=1}^n f(k/n) - \int_0^1 f(t) dt \right|\\&=  \left| \sum_{k=1}^n \left( \left(\frac{k}{n} - \frac{k-1}{n}\right)f(k/n) - \int_{\frac{k-1}{n}}^{\frac{k}{n}} f(t) dt\right)\right|\\ & =\left|\sum_{k=1}^n  \int_{\frac{k-1}{n}}^{\frac{k}{n}} (f(k/n) -f(t)) dt\right|\\ &\leq \sum_{k=1}^n  \int_{\frac{k-1}{n}}^{\frac{k}{n}} \left|f(k/n) -f(t)\right| dt\\ &\leq \sum_{k=1}^n  \int_{\frac{k-1}{n}}^{\frac{k}{n}}\sup_{s\in [(k-1)/n, k/n]}|f'(s)| \left|k/n-t\right| dt\\ &\leq \sup_{s\in [0,1]}|f'(s)| \sum_{k=1}^n   \int_{\frac{k-1}{n}}^{\frac{k}{n}} \frac{1}{n} dt = \frac{1}{n} \sup_{s\in [0,1]}|f'(s)| = \frac{1}{n}.\end{align*}

La convergence est du même ordre que celle obtenue par la série alternée. Elle est très lente.

Remarque : Cette méthode est générale et marche car $f$ est $C^1$. Plus généralement on a que \[\left|S_n(f)- \int_a^b f(t) dt\right| \leq\sup_{s\in [0,1]}|f'(s)|\frac{b-a}{n}.\]

Digression autour du post sur ln(2) - série entière

Dans le post sur $\ln(2)$, on a vu que le développement de Taylor convergeait très lentement. Il convient alors de commenter ce manque de convergence.

On pose $f(z)= \sum_{k=1}^\infty a_n z^n$ la série entière donnée par $a_n=1/n$. On rappelle que le rayon de convergence est donné par :
\[R = \sup\left\{|z|: z\in\mathbb{C},\sum a_n z^n \text{ converge simplement }\right\}\in\, [0,+\infty].\]

Tout d'abord on a vu ici que $f(-1)= -\ln(2)$, donc le rayon de convergence est plus petit ou égal à $1$. D'un autre côté $f(1)$ n'existe pas, c'est la série harmonique qui diverge. Donc le rayon de convergence est plus grand ou égal à $1$. Il vaut exactement $1$.

On aurait pu trouver le rayon de convergence en utilisant le critère d'Alembert. On peut aller ici pour se rafraichir la mémoire. 

En effet on a $\lim_{n\to \infty} \frac{a_n}{a_{n+1}}=1 = 1/R$.

On sait aussi que la série donnée par $f(z)$ converge absolument pour tout $z\in D(0, R)$, disque ouvert de rayon $R$. En particulier si $z$ est dans ce disque, $C(z):=\sup_n |a_n| |z^n|<\infty$, car le terme général d'une suite convergente est borné (et tend vers $0$). 

On pose $f_N(z):= \sum_{k=1}^N a_n z^n$ et on regarde sa vitesse de convergence vers $f(z)$. On utilise une couronne de sécurité. On a que $|z|<(|z|+R)/2<R$. On voit : 

\begin{align*} |f(z)- f_N(z)|&\leq \sum_{k=N+1}^\infty |a_n| \left(\frac{|z|+R}{2}\right)^n \left(\frac{2|z|}{|z|+R}\right)^n\leq C(z) \sum_{k=N+1}^\infty \left(\frac{2|z|}{|z|+R}\right)^n \\&=C(z)\frac{\left(\frac{2|z|}{|z|+R}\right)^{N+1}}{1- \left(\frac{2|z|}{|z|+R}\right)}\end{align*}

Car c'est une suite géométrique de raison strictement plus petite que $1$. 

La convergence à l'intérieur du disque de convergence de la somme partielle d'ordre $N$ vers sa limite est donc de l'ordre de $N+1$. Cela est rapide. 

Dans le post sur $\ln(2)$, la lenteur de la convergence des sommes partielles vient du fait que l'on est sur le bord du disque de convergence.

Approximation de ln(2)

Nous utilisons maintenant la formule de Taylor avec reste intégrale qu'on vient de revoir. Il y a deux grands exercices classiques. Le premier est pour montrer que la somme exponentielle converge bien vers l'exponentielle (qui est par exemple définie par une équation différentielle). Par exemple cela est fait ici.

---

Avant de passer à Taylor à l'ordre $n$, il convient de trouver la dérivée $n$-ième de $x\mapsto \ln(1+x)$.

---

Ici, la récurrence ne pose pas de problème technique. Cependant, il est important d'éviter les horreurs telles que $(f(x))'$ qui vaut $0$ (car c'est une constante !!) et non $f''(x)$. 

---

---

On écrit ensuite la formule de Taylor avec reste intégral.

---

La photo est malheureusement floue. Ici on estime le reste intégral. On majore en mettant la valeur absolue sous l'intégrale.

---

Il est hors de question de calculer cette intégrale car elle vaut $\ln(2)$ moins la somme et nous apporte donc rien, on retourne sur nos pas. On fait une majoration. 

Quand un quotient doit être majoré, on a "deux" choix. On peut majorer le numérateur ou minorer le dénominateur. Ici il est remarquable que les deux méthodes permettent de conclure.

---

On choisit la meilleure des deux majorations. Il convient de se souvenir de citer le théorèmes des gendarmes pour être complet. 

---

On passe ensuite à une application numérique. Pour être précis à $10^{-9}$, il suffit de calculer la somme jusqu'au terme $10^9+1$-ième. Cette méthode est très mauvaise d'un point de vue numérique...

Remarque : On rappelle que la suite $S_n:= \sum_{k=1}^n (-1)^k a_k$ converge si $\lim_{k\to \infty} a_k =0$ (ici $a_k= -1/k$ et tend vers $0$). On appelle $S$ sa limite. C'est une série alternée. De plus, on a que $|S-S_n| \leq |a_{n+1}|$. 

On voit donc que la convergence et l'estimation de la vitesse de convergence aurait pu être obtenue en invoquant la théorie des séries alternées. Cependant, la théorie ne donne pas la limite mais juste une valeur approchée. C'est là qu'intervient l'approche de Taylor avec reste intégral.

Formule de Taylor avec reste intégral

Le but de ce post est de redémontrer la formule de Taylor avec reste intégral en la conjecturant tout d'abord puis la démontrant par récurrence.

Avec l'hypothèse $C^1$, on peut utiliser le théorème fondamentale de l'analyse. On rappelle ici qu'on utilise l'intégrale de Riemann dans le contexte du CAPES.

Pour la deuxième ligne, on utilise l'hypothèse $C^2$ et on fait une intégration par partie. 

Attention ici il y a une astuce. Il faut choisir la bonne primitive pour la fonction constante $1$ et pas prendre bêtement $t\mapsto t$.

---

On continue notre développement de Taylor. On utilise maintenant l'hypothèse $C^3$. Ici encore, on utilise pas la primitive canonique.

---

On passe maintenant à la conjecture. On pose l'hypothèse de récurrence. J'attire votre attention sur le fait que l'hypothèse $f \in C^{n+1}(I)$ est dans $P_n$.

---

Ici, il y a point qui semble déroutant de prime abord. Contrairement à beaucoup des récurrences, ici on commence pas en citant $P_n$. On fait tout d'abord l'hypothèse $f\in C^{n+2}(I)$, qui fait partie de $P_{n+1}$, puis on invoque $P_n$ qui est valide car $f\in C^{n+1}(I)$ en particulier.

---

On peut enfin conclure.

Association Croc en Jambe à l'IMB

Fresque réalisée par l'association Croc en Jambe lors de la journée de rentrée de l'institut de mathématiques de Bordeaux.