Nous continuons le brassage des techniques de calculs (qui ne sera pas exhaustive...) de $\ln(2)$. On a vu dans le post précédent que l'on peut voir
\[\ln(2)=\int_0^1 \frac{1}{1+x}dx.\]
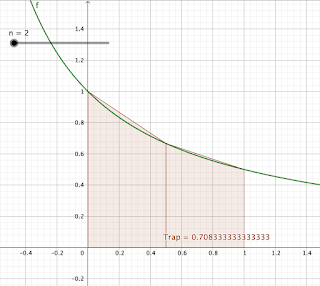
Parlons rapidement de la méthode des trapèzes. Comme on peut le deviner, au lieu d'approcher l'aire à l'aide de rectangles, on s'aide de trapèzes. On peut consulter wiki pour une introduction.
\[\ln(2)=\int_0^1 \frac{1}{1+x}dx.\]
Il y existe toute une "jungle" de méthode d'approximation pour le calcul d'une intégrale. Stricto-senso, les sommes de Riemann sont au programme de l'écris du CAPES et pas les autres méthodes.
Parlons rapidement de la méthode des trapèzes. Comme on peut le deviner, au lieu d'approcher l'aire à l'aide de rectangles, on s'aide de trapèzes. On peut consulter wiki pour une introduction.
Ces deux méthodes sont implémentées dans geogebra : SommeRectangles et SommeTrapèzes.
Etant donnée une fonction $f$ continue sur $[a,b]$, pour $\int_a^b f(x)\,dx$, avec $n\in \mathbb{N}$, on l'approche par
\[S_n(f):=\frac{b-a}{n} \left( {f(a) + f(b) \over 2} + \sum_{k=1}^{n-1} f \left( a+k \frac{b-a}{n} \right) \right)\]
Si $f\in C^2([a,b])$, grâce au théorème des accroissements finis, il n'est pas très difficile de montrer que
\[\left|\int_a^b f(x)\,dx - S_n(f) \right| \leq \frac{(b-a)^3}{12n^2}\max_{x\in [a,b]}|f''(x)|.\]
Contrairement à la méthode des rectangles, celle-ci est d'ordre $2$. Cependant elle s'appuie sur une hypothèse un peu plus forte, $C^2$ au lieu de $C^1$.
Revenons à notre exemple fil rouge. On a
\[S_n^{trap}:=\frac{1}{n} \left( \frac{3}{4} + \sum_{k=1}^{n-1} \frac{1}{1+ \left( \frac{k}{n} \right) }\right) = \frac{3}{4n} + \sum_{k=1}^{n-1} \frac{1}{n+ k}\]
avec une erreur de
\[\frac{1}{6n^2}.\]
Pour avoir une précision à $10^{-9}$ près il suffit de prendre $n\geq \sqrt{10^9/6}\geq 12910$. Cela est vraiment meilleur que pour la méthode des rectangles qui demandait $10^9$ termes pour la même précision. Cependant, cela reste encore très grand comme nombre.
On rappelle qu'avec la méthode des rectangles on avait obtenu:
\[S_n^{rect}:=\sum_{k=1}^{n} \frac{1}{n+ k}.\]
Si l'on compare les deux on obtient:
\[S_n^{trap} = S_n^{rect} -\frac{1}{4n}.\]
On peut résumer cette comparaison par :
\begin{align*}\ln(2)&= \sum_{k=1}^{n} \frac{1}{n+ k} + O\left(\frac{1}{n}\right)\\ &=-\frac{1}{4n} + \sum_{k=1}^{n} \frac{1}{n+ k} + O\left(\frac{1}{n^2}\right), \end{align*}
quand $n\to \infty$. Cela rappelle fortement un développement limité...
Pour aller plus loin on pourra par exemple consulter le site de Serge Mehl et regarder la méthode de Simpson qui est d'ordre 4.

Aucun commentaire:
Enregistrer un commentaire