Tout d'abord quelques références :
Il y a beaucoup de méthodes pour calculer le DL de la fonction tangente en 0. Nous procédons ici par utilisation d'une équation différentielle ordinaire. On remarquera que cette méthode permet d'avoir un DL sans connaître explicitement la solution de l'équation.
- Vous avez ici des exemples vidéos de DL sous forme de produit et de composition.
- Vous avez ici un exemple vidéo avec un quotient.
- Vous avez ici et là une série d'exercices corrigés de différents niveaux.
Il y a beaucoup de méthodes pour calculer le DL de la fonction tangente en 0. Nous procédons ici par utilisation d'une équation différentielle ordinaire. On remarquera que cette méthode permet d'avoir un DL sans connaître explicitement la solution de l'équation.
L'approche ici est de type bootstrap. On peut traduire ce terme par auto-amélioration. On va partir un certain DL, le rentrer dans l'équation et obtenir un DL pour la dérivé. Cela donnera alors un DL à un ordre supérieur pour la fonction (par intégration du DL). Puis on recommence.
Cela est similaire à la machine pour fabriquer des pâtes ! (vidéo)
Quand on intègre un DL, il ne faut par oublier la constante d'intégration qui est simplement la valeur au point de la fonction qu'on développe.

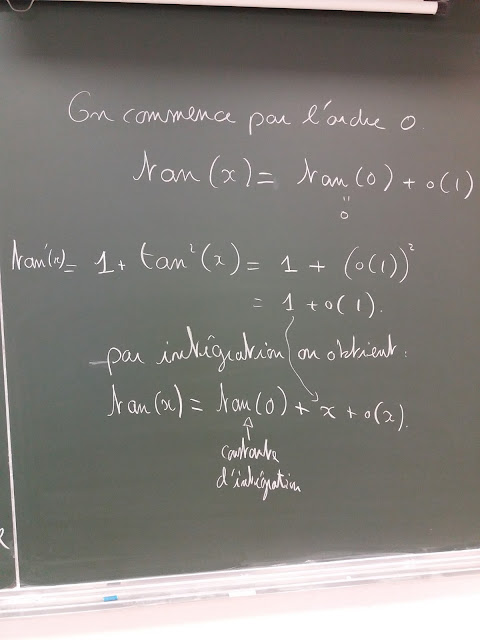

Aucun commentaire:
Enregistrer un commentaire